
Study Site on the Western Side of Tucson
Abstract: The objective of this experiment was to observe the ecological relationship between triangle-leaf bursage (Ambrosia deltoidea) and krameria (Krameria grayi). The purpose was to see if krameria is potentially parasitic, as it survives more often in the presence of another desert plant species. This is also known as the “hemiparasite hypothesis.” We also compared these results to creosote (Larrea tridentata), a plant we hypothesized to not be parasitic. To test these hypotheses, we walked along transects and tallied the number of krameria and creosote on our paths. We additionally recorded whether these plants were associated with triangle-leaf bursage or not. The data revealed that for both creosote and krameria, most plants were associated. These results indicate that the alternative hypothesis that krameria is parasitic is true. Nonetheless, considering that creosote is not parasitic, a sampling error likely occurred due to the low plant cover estimate in the study region. In conclusion, being able to distinguish between parasitic and non-parasitic species in the desert may help shed light on biological communities at higher trophic levels.
The Ecological Relationship Between Hemiparasite Krameria grayi and its Host, Ambrosia deltoidea
Note: This paper is the work of both myself and a colleague of mine, but her name has been removed from the report for the sake of privacy.
Chi-Square Test Description:
One technique that was utilized in this study is the chi-square test; this is a way for researchers to determine whether the outcome from an experiment is “significant” or not. Simply put, a result is considered significant if the outcome matches the predictions of the alternative hypothesis, but not those of the null hypothesis. An alternative hypothesis is a proposed explanation for an observation(s), while the null hypothesis encompasses everything that is true if the alternative is false. For example: for this study, one of the alternative hypotheses was that krameria is parasitic (given the observation that this plant is often seen together with other species). Consequently, the null was that krameria is not parasitic. Because our results indicated that krameria is in fact parasitic, we accepted the alternative, rejected the null, and thus considered the outcome to be “significant.”
In order to determine if a result is indeed significant, several calculations need to be performed. This is done using the observed values and those values that are expected if the alternative were false/null were true. Additionally, the method of calculation of expected values will differ depending on the experiment. For this particular research, percent coverage, which was 13.27%, of triangle-leaf bursage (the host plant) at the study site was utilized to obtain these expected values. If the null were true and krameria were not parasitic, it should have been evenly distributed amongst the entire study area without showing any particular affiliation to triangle-leaf bursage. Thus, we multiplied the total number of krameria counted (979 plants) by 0.1327 and 0.8673 (1 – 0.1327) to obtain the expected values of krameria associated and not associated with the host species. The observed values, in turn, were simply how many krameria were indeed associated or not associated with triangle-leaf bursage.
The next step is to perform another calculation using the following formula:
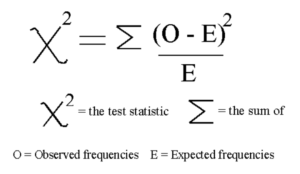
Link to Source: http://www.theseashore.org.uk/theseashore/Stats%20for%20twits/Chi-Squared.html
For example: for krameria associated with triangle-leaf bursage, the observed number was 620 while the expected value (again, if the null hypothesis were true) was 129.9 plants. Plugging these numbers into the equation above gives a value of 1,849.1. These steps were then repeated for krameria not associated with triangle-leaf bursage, which ultimately gave a value of 282.9. Finally, these two numbers were added together to give an “x2” value of 2,132.
The last step in the chi-square test requires the use of a table of predetermined values to compare one’s obtained “x2” value to:
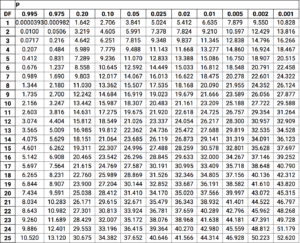
Link to Full Table: https://www.medcalc.org/manual/chi-square-table.php
The “DF” column on the left side of the table stands for “degrees of freedom.” This is a measurement of how many different possibilities there are for an outcome. To obtain how many degrees of freedom there are for a particular experiment, one must subtract a value of one from the number of possible “categories” of information that can vary. For example: when counting the number of krameria, there are two categories; the plant may either be associated or not associated with triangle-leaf bursage. That gives a value of two. After a value of one is subtracted, we end up with one degree of freedom. Therefore, we look at the table under the “1” row and find where our calculated “x2” value (2,132) lies. Any number greater than the value under P=0.05 is considered a “significant” outcome. Upon examining the table, we find that the number under P=0.05 for one degree of freedom is 3.841. Obviously, 2,132 is a much larger number. Thus, because the result is significant, we accept our alternative hypothesis that krameria is parasitic and reject the null hypothesis.